opgaver:Uge1

Disse statistik-øvelser er redigerede udgaver af opgaverne 3.4, 3.25, 4.6, 4.28, 5.11 og 5.31 fra R. J. Taylor's An Introduction to Error Analysis.

Det er meningen af så meget som muligt af opgaverne skal laves i MATLAB.

Opgave 1 - Tælletal

Når en prøve med radioaktive atomer henfalder, vil antallet af radioaktive atomer falde, og prøvens radioaktivitet vil falde proportionalt med dette. For at undersøge denne effekt måler en fysiker på partiklerne der udsendes fra en radioaktiv prøve i løbet af to timer. Hun tæller antallet af partikler der udsendes i løbet af en 1 minut lang periode med halve timers intervaller, med følgende resultater:

Tid gået, $t$ (timer):	0.0	0.5	1.0	1.5	2.0
Antal tællinger, $\nu$, på 1 minut:	214	134	101	61	54

Spørgsmål a

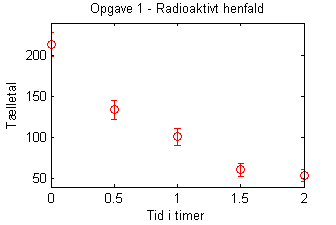
Brug MATLAB til at plotte antallet af tællinger imod den tid der er gået. Inkludér errorbars for at vise usikkerheden på tallene. (Negligér usikkerheder i den tid der er gået).

Hint 

For en hjælp til hvordan man plotter data, se "MATLAB® Primer" (tidligere kaldet "Getting Started with MATLAB") guiden, der ligger på Absalon. Kapitel 4 indeholder en masse plotning generelt. Prøv at slå funktionen errorbar op i MATLAB hjælpen bagefter.

Løsning 

Plottet som det burde se ud efter at have kørt denne kode.

For at plotte datapunkterne med usikkerheder skal data først indlæses. Usikkerhederne er kvadratroden af tælletallet, så

t = 0:0.5:2;

nu = [214 134 101 61 54];

nu_usikk = sqrt(nu);

Herefter kan data plottes vha. MATLAB funktionen errorbar(x,y,e), der plotter $(x,y)$ data, hvor der er usikkerheden $e$ på $y$-dataen. En figur åbnes med

figure

der plottes med

errorbar(t,nu,nu_usikk,'ro')

og til sidst laves der en

hold on

for at blive ved med at plotte oven i det allerede lavede (ellers vil de næste kommandoer overskrive errorbar plottet). Jeg sætter nu også akser, titel og akselabels med

axis([-0.5 2.5 40 240])

title('Opgave 1 - Radioaktivt henfald')

xlabel('Tid i timer')

ylabel('Tælletal')

Spørgsmål b

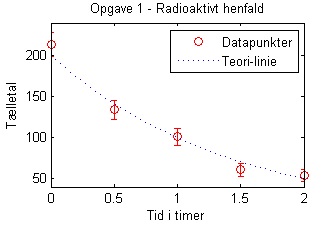
En teori forudsiger at antallet af udsendte partikler burde falde eksponentielt ved $\nu = \nu_0 \exp{(-rt)}$, hvor der (i dette tilfælde) gælder at $\nu_0 = 200$ og $r = 0.693 \,\text{hr}^{-1}$. Plot denne forventede kurve på din graf oven på din tidligere graf, og kommentér på hvor godt data ser ud til at passe med den teoretiske forudsigelse.

Hint 

For at plotte en funktion skal man først definere sin førsteakse som en vektor, f.eks. x = 0:0.01:1. Man kan også bruge linspace(x,y,n) funktionen til at lave en liste fra $x$ til $y$ med $n$ punkter. Antallet af punkter definerer opløsningen på det plot man vil lave.

Herefter kan man udregne sine værdier til andenaksen som sin funktion af førsteakseværdierne, f.eks. y = sin(x).

Løsning 

Det endelige plot, der sammenligner data med usikkerheder med en teoretisk linje.

Man definerer linjen for teorien rent numerisk ved at lave en tids-akse som man selv bestemmer hvor detaljeret er, f.eks.

tt = -0.25:0.01:2.25;

og så kan man udregne den teoretiske linje ved

nu_0 = 200;

r = 0.693;

nu_exp = nu_0 * exp(-r*tt);

Hvis man huskede sin hold on tidligere burde man nu bare kunne plotte oven i sit errorbar plot med

plot(tt,nu_exp,'b:')

Som en sidste krone på værket kan man tilføje en legend med

legend('Datapunkter','Teori-linje')

Prøv at lave plottet igen med forskellige layouts af punkterne og linjen. F.eks. er der de forskellige farver r (rød), g (grøn), b (blå), y (gul), m (magenta) og k (sort); punkttyperne . (lille prik), x (krydser), o (store prikker) og * (stjerner); og linjetyperne - (solid), : (prikker) og -- (stiplet), og selvfølgelig mange flere. Prøv at finde disse options i MATLAB hjælpen under LineSpec.

Du kan også lege med egenskaber som MarkerSize, LineWidth, MarkerEdgeColor og MarkerFaceColor for at gøre linjen og punkterne mere tydelige.

Bonus

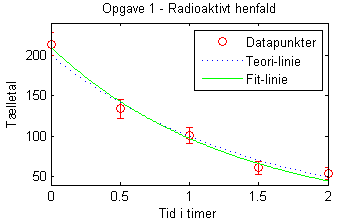
I uge 3 skal I lære hvordan man fitter en funktion til datapunkter i MATLAB - så i stedet for at plotte en given kurve vil I skulle plotte den bedst fittede kurve til data.

Læs mere 

Plottet som før, men nu også med en fit-linje.

Lad os sige at data allerede er indlæst i variablene t og nu (med usikkerhed nu_usikk), som ovenfor. Disse er også allerede plottet som det blev gjort i spørgsmål a.

For at kunne fitte en linje skal man selvfølgelig først definere sin fitte-kurve, der i dette tilfælde vil være $\nu = \nu_0 \exp{(-rt)}$, hvor $\nu_0$ og $r$ nu er fitte-parametre. En funktion kan defineres på mange måder i MATLAB, men når man fitter med simple funktionsudtryk i MATLAB er det nemmest simpelthen bare at fodre fitte-rutinen med den direkte.

cfun = fit(t',nu','a*exp(-b*x)')

Bemærk at t' betyder den transponerede af t. Funktionen fit kræver nemlig søjlevektorer som data, ikke rækkevektorer, som både t og nu er defineret som. Objektet cfun indeholder nu information om fittet, og man kan plotte kurven med de bedste værdier af a og b med

plot(tt,cfun(tt),'g-')

man kan også få parametrene ud ved at kalde variablene cfun.a og cfun.b. Det er også muligt at gå dybere ned i cfun objektet, men dette skal ikke uddybes her.

Bemærk også at ovenstående ikke fodrer MATLAB med et start-gæt på de to fitte-parametre. Dette bør man normalt gøre, da programmet ellers vælger tilfældige startpunkter, og her ikke altid vil konvergere. Man kan gøre det ved at bruge StartPoint option'en, og dette vil vi komme ind på senere.

Opgave 2 - Usikkerheden af et potensudtryk

Fra Barlow's regel (4.10) om usikkerheder af funktionsudtryk, ved vi at et $q = x^2$ har en relativ usikkerhed der er dobbelt så stor som den relative usikkerhed i $x$;

$ \dfrac{\sigma_q}{q} = 2 \dfrac{\sigma_x}{x} . $

Overvej nu det følgende (forkerte) argument: Vi kan tænke på $x^2$ som $x$ gange $x$, så

$ q = x \times x; $

derfor vil der ifølge Barlow's regel (4.14) gælde at

$ \dfrac{\sigma_q}{q} = \sqrt{ \left( \dfrac{\sigma_x}{x} \right)^2 + \left( \dfrac{\sigma_x}{x} \right)^2 } = \sqrt2 \dfrac{\sigma_x}{x} . $

Denne konklusion er forkert. Forklar hvorfor.

Bonus: Prøv at undersøge dette i MATLAB ved at sammenligne den relative usikkerhed (SD divideret med gennemsnitsværdien) for en række af tilfældige tal med den relative usikkerhed på samme række af tal kvadreret. Du kan evt. læse i MATLAB-hjælpen hvad funktionen randn gør.

Hint 

Se på hvad antagelserne for at formel (4.14) gælder faktisk er - passer dette med hvad der arbejdes med i denne opgave?

For at se på det i MATLAB kan man generere en række tilfældige tal vha. randn funktionen. Slå den op i MATLAB hjælpen og se hvad den kan.

Løsning 

Konklusionen i den fejlagtige udledning er forkert fordi man har brugt udtrykket i formel (4.14) uden at overholde dennes antagelser - nemlig at de variable man ganger sammen er uafhængige. Og nu er $x$ jo fuldkommen afhængig af sig selv - hvorfor konklusionen altså kun kan være forkert.

For at se på dette i MATLAB kan man starte med at lave en liste med normalfordelte tal

x = 10 + randn(1,500);

Bemærk at der lægges 10 til, da vi gerne vil dividere med gennemsnittet senere (og at dividere med nul er jo ikke så godt!).

Man kan nu helt manuelt se på den relative usikkerhed på x og på x i anden potens, ved at bruge de indbyggede MATLAB funktioner for standardafvigelse og gennemsnit, std og mean:

std(x)/mean(x)

std(x.^2)/mean(x.^2)

Man finder at nummer to usikkerhed ovenfor ligner at man ganger den første med 2, ikke med $\sqrt{2}$, ved at sammenligne

2*std(x)/mean(x)

sqrt(2)*std(x)/mean(x)

Og dermed er det altså også rent numerisk vist at den naive fremgangsmåde ikke er sand.

Opgave 3 - Flere tælletal

I Barlow kap. 3.3.1 kan I læse at i et tælleeksperiment er usikkerheden på en tælling givet af "kvadratrods-reglen" til at være kvadratroden af tallet. Denne regel kan gøres mere præcis med følgende udsagn: Hvis man tager adskillige tællinger

$ \nu_1, \nu_2, \ldots, \nu_N $

af antallet $\nu$ af tilfældige hændelser der sker inden for tidsrummet $T$, så gælder der: (1) det bedste estimat for det sande gennemsnit af hændelser inden for tidsrummet $T$ er gennemsnittet $\overline\nu = \sum \nu_i/N$ af målingerne, og (2) standardafvigelsen (også kaldt SD, for Standard Deviation) af de observerede tal er approksimativt lig med kvadratroden af dette samme bedste estimat; altså, usikkerheden i hver måling er $\sqrt{\overline\nu}$. I specialtilfældet hvor der kun måles én gang, hvor man får et antal tællinger $\nu$, er det bedste estimat $\nu$, mens usikkerheden er kvadratroden $\sqrt\nu$.

En fysiker bruger en Geiger-tæller til at måle antallet af kosmiske partikler der kommer til hans laboratorie i givne to-sekunders intervaller. Han tæller dette tal 20 gange med følgende resultater:

10,	13,	8,	15,	8,	13,	14,	13,	19,	8,
13,	13,	7,	8,	6,	8 ,	11,	12,	8,	7.

Spørgsmål a

Find gennemsnittet og standardafvigelsen (SD) på disse tal vha. MATLAB.

Løsning 

Først defineres datasættet som en enkel liste med

nu = [10 13 8 15 8 13 14 13 19 8 13 13 7 8 6 8 11 12 8 7];

Derefter kan gennemsnittet og SD udregnes enten manuelt eller ved brug af mean funktionen. F.eks.

gn = sum(nu)/length(nu)

std(nu)

Dermed har man gennemsnittet og datasættets faktiske standardafvigelse.

Husk ikke at forvirre standardafvigelsen SD med standardafvigelsen på gennemsnittet (også kaldt SDOM, for Standard Deviation Of the Mean). Hvis man her vil finde SDOM, skal man dividere med kvadratroden af antallet af punkter,

std(nu)/sqrt(length(nu))

Spørgsmål b

Standardafvigelsen på tallene skulle gerne være ca. lig med kvadratroden på deres gennemsnit. Hvor godt passer dette?

Løsning 

Kvadratroden af gennemsnittet udregnes simpelthen med (ved brug af løsningen fra spørgsmål a)

sqrt(gn)

Denne standardafvigelse er faktisk et over-estimat, men den passer ok med den udregnede std(nu) fra ovenfor.

Opgave 4 - Systematiske fejl

Et pendul består af en metalkugle der hænger i en snor. Den effektive længde af pendulet er længden af snoren plus radius af kuglen.

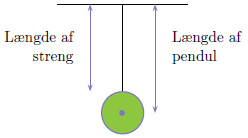
Systematiske fejl kommer nogle gange fra at fysikeren helt uvidende måler det forkerte. Her er et eksempel: En studerende forsøger af måle $g$ ved at bruge et pendul lavet af en stålkugle der hænger i en let snor (se figuren). Han måler fem forskellige længder af pendulet og de tilhørende perioder $T$ som følger:

Længde, $l$ (cm):	51.2	59.7	68.2	79.7	88.3
Periode, $T$ (s):	1.448	1.566	1.669	1.804	1.896.

Spørgsmål a

For hver datapar udregner han $g$ som $g = 4 \pi^2 l/T^2$. Han udregner derefter gennemsnittet af de fem værdier, deres SD, og deres SDOM. Ved at antage at alle hans fejl er tilfældige kan han bruge SDOM som sin endelige usikkerhed, og skriver sit resultat på standardformen gennemsnit $\pm$ SDOM. Find hans resultat for $g$ vha. MATLAB.

Hint 

Start med at opskrive data i to 1D arrays - et array for l og et array for T. Nu kan du udregne g vha. den givne funktion, og lave statistik på denne.

Løsning 

Dataen læses ind med

l = [51.2 59.7 68.2 79.7 88.3];

T = [1.448 1.566 1.669 1.804 1.896];

og tyngdeaccelerationskoefficienten udregnes ved

g = 4*pi^2*l./T.^2

Herefter kan man finde gennemsnittet, SD og SDOM af værdierne vha. de indbyggede MATLAB funktioner

g_mean = mean(g)

sigma = std(g)

sigma_mean = std(g)/sqrt(length(g))

Spørgsmål b

Han sammenligner nu sit resultat med den accepterede værdi $g = 979.6 \,\text{cm}/\text{s}^2$ og forfærdes over at se at hans diskrepans (afvigelse fra den accepterede værdi) er tæt på 10 gange større end hans usikkerhed. Bekræft denne sørgelige konklusion.

Løsning 

Diskrebansen findes bare som forskellen,

g_right = 979.6;

discrepancy = g_mean - g_right

Spørgsmål c

Efter at have gennemtjekket alle sine udregninger konkluderer han at han må have overset en systematisk fejl. Han er helt sikker på at der ikke var problemer med målingen af perioden $T$, så han spørger sig selv: Hvor stor skulle en systematisk fejl i længden $l$ være for at grænserne for den totale usikkerhed lige præcis inkluderer den accepterede værdi $979.6 \,\text{cm}/\text{s}^2$? Vis med MATLAB at svaret er ca. 1 cm.

Hint 

Prøv at lave en udregning hvor du ændrer din værdi for $l$ en lille smule, og se hvor langt du så skal ændre den for at få en $g$ der passer med den korrekte $g$. Det kan evt. være en god idé at se lidt på for-løkker i MATLAB, så programmet kan iterere for dig.

Løsning 

Plot der viser afstanden mellem den accepterede $g$ og den yderste SDOM grænse på den fundne $g$ når der er lagt $x$ til $l$.

For at finde hvor stor fejlen skulle være for at den rigtige værdi er inden for SDOM, kan man lave et loop der lægger lidt ekstra til $l$, og så udregner forskellen mellem den fundne $g$ og den rigtige,

x = 0.1:0.1:1.2;

for i=1:length(x)

g_new = 4*pi^2*(l+x(i))./T.^2;

discr_new(i) = mean(g_new) + std(g_new)/sqrt(length(g_new)) - g_right;

end

Den nemmeste måde at se resultatet på er ved at plotte det

plot(x,discr_new,'.b')

Man kan se at den skærer 0 ca. omkring 1 cm (se figuren), hvilket netop var hvad der skulle vises.

Man kunne selvfølgelig også sammenligne den teoretiske værdi for $g$ med gennemsnits-værdien for sin udregnede $g$, hvilket selvfølgelig bare skal gøres ved at erstatte discr_new udregningen ovenfor med

discr_new(i) = mean(g_new) - g_right;

Spørgsmål d

Dette resultat ville betyde at hans længdemålinger har en systematisk fejl på omkring en centimeter - en konklusion som han først afviser som absurd. Mens han stirrer på pendulet kommer han dog i tanke om at 1 cm er ca. radius af kuglen, og at de længder han har målt var længderne af snoren. Da den korrekte længde af et pendul er afstanden fra fastgørelsespunktet til centrum af kuglen (se figuren), er hans målinger altså systematisk blevet målt forkert med radius af kuglen. Han bruger derfor en skydelære til at måle kuglens diameter, der viser sig at være 2.00 cm. Lav de nødvendige korrektioner til hans data og udregn hans endelige resultat for $g$ med dennes usikkerhed.

Løsning 

For at rette den systematiske fejl kan man bare lægge den ene cm til sine $l$-værdier,

l = l + 1

og så udregner man sin $g$-værdi forfra, ligesom det blev gjort før:

g = 4*pi^2*l./T.^2;

g_mean = mean(g)

sigma_mean = std(g)/sqrt(length(g))

Opgave 5 - Gauss-fordelingen

Plot Gauss-fordelingen (også kaldt normalfordelingen),

$ G_{X,\sigma}(x) = \dfrac{1}{\sigma\sqrt{2\pi}} \exp{\left( -\dfrac{(x-X)^2}{2\sigma^2} \right)} , $

i den samme MATLAB figur for de følgende to sæt af parametre: $X=2$, $\sigma=1$, og $X=3$, $\sigma=0.3$. Tilføj en titel, labels på akserne, og en legend til dit plot, og sammenlign de to grafer.

Løsning 

Plot af to forskellige Gauss-funktioner.

Først definerer man sin $x$-akse, f.eks. ved

x = -2:0.05:6;

Derefter giver man sine parametre

X1 = 2;

sigma1 = 1;

X2 = 3;

sigma2 = 0.3;

til sidst kan man så udregne sine funktionsværdier ved

y1 = 1/( sigma1*sqrt(2*pi) ) * exp(-(x-X1).^2/(2*sigma1^2));

y2 = 1/( sigma2*sqrt(2*pi) ) * exp(-(x-X2).^2/(2*sigma2^2));

Man kunne også definere en funktion for sin Gauss-fordeling ved definitionen

MinGauss = @(x,a,b) 1/( b*sqrt(2*pi) ) * exp(-(x-a).^2/(2*b^2));

og med denne kan man bare skrive

y1 = MinGauss(x,X1,sigma1);

y2 = MinGauss(x,X2,sigma2);

Til sidst plotter man de to funktioner sammen. Her kan man bruge at plot godt kan finde ud af at plotte flere funktioner af gangen:

plot(x,y1,'r-',x,y2,'b-')

Opgave 6 - Binning

I den følgende liste er der 40 målinger $t_1,\ldots,t_{40}$ af tiden det tager en sten at falde fra et vindue til jorden (alle i hundrededele sekunder):

63	58	74	78	70	74	75	82	68	69
76	62	72	88	65	81	79	77	66	76
86	72	79	77	60	70	65	69	73	77
72	79	65	66	70	74	84	76	80	69

Spørgsmål a

Brug MATLAB til at udregne standardafvigelsen $\sigma_t$ for alle 40 målinger.

Løsning 

Først og fremmest skal datasættet lige indlæses,

t = [63 58 74 78 70 74 75 82 68 69 76 62 72 88 65 81 79 77 66 76 86 72 79 ...

77 60 70 65 69 73 77 72 79 65 66 70 74 84 76 80 69];

Standardafvigelsen findes så simpelt med den indbyggede MATLAB funktion,

std(t)

Spørgsmål b

Udregn gennemsnittene $\overline t_1,\ldots,\overline t_{10}$ af fire målinger af gangen (f.eks. af de fire målinger i hver af de 10 kolonner, eller af fire nabo-tal ad gangen). Du kan tænke på dataen som om den kom fra 10 eksperimenter, hvor man i hvert eksperiment fandt gennemsnittet af fire tidsmålinger. Givet resultatet i del (a), hvad forventer du så at standardafvigelsen på de 10 gennemsnit $\overline t_1,\ldots,\overline t_{10}$ er? Udregn den.

Løsning 

For at binne med fire målinger af gangen er det nemmest at arbejde med et loop der gør det automatisk for dig. For at bruge et generelt antal punkter at binne med defineres tallet først:

ncol = 4;

Herefter startes der to tomme arrays op - et til gennemsnittene, og et til standardafvigelserne (zeros(n,m) laver et $n\times m$ array der indeholder nuller i alle elementer):

gn = zeros(1,10);

sd = zeros(1,10);

Et loop laver udregningerne:

for n = 0:9

gn(n+1) = sum(t(n*ncol+1:n*ncol + ncol))/ncol;

sd(n+1) = std(t(n*ncol+1:n*ncol + ncol));

end

Man kan så endelig se gn og sd ved simpelthen at printe dem ud via kommandolinjen.

Ud fra del (a) ville man forvente at SD er fordelt omkring den SD man fandt tidligere, og det er også det der sker.

Spørgsmål c

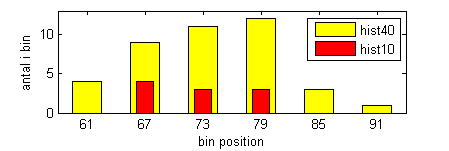
Plot histogrammer for både de 40 individuelle målinger $t_1,\ldots,t_{10}$ og de 10 gennemsnit $\overline t_1,\ldots,\overline t_{10}$. Brug de samme skalaer og bin størrelser for begge plot, så de kan sammenlignes. Hvad forventer du af de to histogrammer, og ser de faktisk sådan ud?

Løsning 

De to histogrammer til sammenligning.

For at plotte histogrammer der kan sammenlignes skal man bruge histc, hvor man kan vælge bin-grænser manuelt. Histogrammerne laves ved først at definere grænserne for bins'ene ved

nbins = 5;  %antal bins

min = 58;  %position af første bin grænse

dist = 6;  %bredde af bins

max = min+nbins*dist;

edges = min:dist:max;

For at kunne plotte bins'ene med en korrekt førsteakse skal man også finde centrum af hvert bin. Dette gøres med

centers = min+dist*0.5:dist:max+dist*0.5;

Herefter udregnes histogrammerne med

hist40 = histc(t,edges);

hist10 = histc(gn,edges);

og de kan nu plottes med bar funktionen,

figure

bar(centers,hist40,0.5,'y')

hold on

bar(centers,hist10,0.3,'r')

Man kan tydeligt se at hist10 er mere centreret, som forventet.

Samlede løsninger

• Et samlet dokument med MATLAB kode til at løse alle opgaverne ovenfor kan hentes her: opgaver_uge1_2_taylor.m