opgaver:Uge3
Pia Jensen (Talk | contribs) |
Pia Jensen (Talk | contribs) |
||
| Line 33: | Line 33: | ||
For at få usikkerheder på punkterne, kan du starte med at lave et array af samme størrelse som dit datasæt, der indeholder usikkerhederne for hvert punkt (her bare den samme usikkerhed for alle punkter) | For at få usikkerheder på punkterne, kan du starte med at lave et array af samme størrelse som dit datasæt, der indeholder usikkerhederne for hvert punkt (her bare den samme usikkerhed for alle punkter) | ||
| + | [[File:uge3fig1.png|frame|Modellen vist som en linie, sammen med genererede data med støj.]] | ||
:<code>sigma_y = sigma*ones(size(y_model));</code> | :<code>sigma_y = sigma*ones(size(y_model));</code> | ||
| Line 41: | Line 42: | ||
Nu kan du plotte din model sammen med dine "målepunkter", | Nu kan du plotte din model sammen med dine "målepunkter", | ||
| − | |||
:<code>figure</code> | :<code>figure</code> | ||
:<code>errorbar(x,y,sigma_y,'bo','MarkerFaceColor', [0.4 0.4 0.8],...</code> | :<code>errorbar(x,y,sigma_y,'bo','MarkerFaceColor', [0.4 0.4 0.8],...</code> | ||
| Line 51: | Line 51: | ||
En sådan figur er vist her til højre. | En sådan figur er vist her til højre. | ||
| + | |||
| + | [[File:uge3fig2.png|frame|Modellen og datapunkterne med støj, nu med en fit-linie (grøn).]] | ||
| + | Regressionsparametrene kan udregnes med | ||
| + | |||
| + | :<code>N = length(x);</code> | ||
| + | :<code>Sy = sum(y);</code> | ||
| + | :<code>Sx = sum(x);</code> | ||
| + | :<code>Sxx = sum(x.^2);</code> | ||
| + | :<code>Sxy = sum(x.*y);</code> | ||
| + | :<code>Delta = N*Sxx-Sx^2;</code> | ||
| + | :<code>A_fit = ( Sxx*Sy - Sx*Sxy )/Delta;</code> | ||
| + | :<code>B_fit = ( N*Sxy - Sx*Sy )/Delta;</code> | ||
| + | |||
| + | og fit-linien er så fundet til at være | ||
| + | |||
| + | :<code>y_fit = A_fit + B_fit*x;</code> | ||
| + | |||
| + | Denne linie plottes oven på model-linien og punkterne med | ||
| + | |||
| + | :<code>plot(x,y_fit,'g-','LineWidth',2)</code> | ||
| + | |||
| + | og så får man figuren til højre. | ||
:<code></code> | :<code></code> | ||
{{hidden end}} | {{hidden end}} | ||
Revision as of 17:04, 6 March 2012
I denne opgave skal I arbejde med fitning som forklaret i Taylor kapitel 8. I skal her selv lave et datasæt, og lærer derfor også hvordan man genererer tilfældige tal i MATLAB. Opgave 2 og 3 er uafhængige, og kan laves i den rækkefølge I har lyst til.
Contents |
Opgave 1 - Fitning
Spørgsmål 1 - Lineær model
Antag at I har en lineær model som i Taylor afsnit 8.2,
- $y = A + B x .$
Vælg passende værdier af A og B og lav en vektor x med målepunkter, f.eks. A = 0, B = 1, x = -2:0.1:2. Lav nu en vektor med den "sande" y ud fra modellen. Vælg en usikkerhed for målingerne, og læg en normalfordelt støj til hver måling - brug MATLAB funktionen randn(). Plot målingerne (med usikkerhederne) og den "sande" model i samme plot.
Beregn lineær regression ud fra Taylor og find de estimerede værdier for A og B, og beregn den fittede modelværdi, y_fit. Plot y_fit oveni det forrige plot og se hvor godt fittet er. Beregn den reducerede $\chi^2$, givet ved
- $\dfrac{\chi^2}{N-P} ,$
hvor $N$ er antal datapunkter og $P$ er antal fit-parametre.
Start med at udregne selve den teoretiske linie y_model, ved at definere A, B og din x-akse. Definér derefter en sigma du vil bruge som din usikkerhed. Så kan din y udregnes som y_model plus en vektor der består af Gaussisk fordelte tal med spredning sigma og centrum nul.
Start med at definere de to konstanter, din x-akse og den usikkerhed du gerne vil have på punkterne, her f.eks.
A_model = 0;B_model = 1;sigma = 0.5;x = -2:0.1:2;
Nu kan du udregne modellens y-værdi direkte ved
y_model = A_model + B_model*x;
For at få usikkerheder på punkterne, kan du starte med at lave et array af samme størrelse som dit datasæt, der indeholder usikkerhederne for hvert punkt (her bare den samme usikkerhed for alle punkter)
sigma_y = sigma*ones(size(y_model));
Herefter udregner du dine y-værdier med støj på ved at bruge randn() funktionen
y = y_model + sigma_y.*randn(size(y_model));
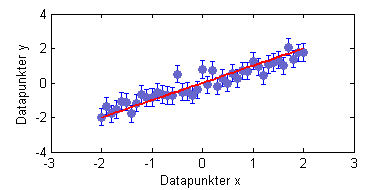
Nu kan du plotte din model sammen med dine "målepunkter",
figureerrorbar(x,y,sigma_y,'bo','MarkerFaceColor', [0.4 0.4 0.8],...'MarkerEdgeColor',[0.4 0.4 0.8])
hold onplot(x,y_model,'r-','LineWidth',2)xlabel('Datapunkter x')ylabel('Datapunkter y')
En sådan figur er vist her til højre.
Regressionsparametrene kan udregnes med
N = length(x);Sy = sum(y);Sx = sum(x);Sxx = sum(x.^2);Sxy = sum(x.*y);Delta = N*Sxx-Sx^2;A_fit = ( Sxx*Sy - Sx*Sxy )/Delta;B_fit = ( N*Sxy - Sx*Sy )/Delta;
og fit-linien er så fundet til at være
y_fit = A_fit + B_fit*x;
Denne linie plottes oven på model-linien og punkterne med
plot(x,y_fit,'g-','LineWidth',2)
og så får man figuren til højre.
Spørgsmål 2 - Gentagelse
Gentag dette "numeriske forsøg" et antal gange (f.eks. 100) og gem for hver gang fittets parametre. Brug hist() til at finde fordelingen af A, B, og reduceret $\chi^2$. Sammenlign med den estimerede usikkerhed på A og B, og undersøg evt. korrelationen mellem A og B (plot f.eks. A vs. B).
Spørgsmål 3 - Automatisk fitning i MATLAB
Prøv at anvende MATLABs fittefunktion fit(x,y,'funktion') og sammenlign med jeres egen lineære regression.