opgaver:Uge5
Pia Jensen (Talk | contribs) |
Pia Jensen (Talk | contribs) |
||
| Line 179: | Line 179: | ||
| − | == Opgave 3 - | + | == Opgave 3 - Principal component analysis == |
| − | Disse øvelser handler om radial acceleration (med Principal Component Analysis). | + | Disse øvelser handler om radial acceleration (med Principal Component Analysis - PCA). |
* Du skal starte med at hente datasættet [[Media:ipod_4.txt|ipod_4.txt]], der er et datasæt taget med app'en [http://www.iseismometer.com/ iSeismometer] på en Ipod Touch som del af et eksperiment på kurset i 2011. | * Du skal starte med at hente datasættet [[Media:ipod_4.txt|ipod_4.txt]], der er et datasæt taget med app'en [http://www.iseismometer.com/ iSeismometer] på en Ipod Touch som del af et eksperiment på kurset i 2011. | ||
| Line 187: | Line 187: | ||
Indlæs datasættet. De fire variable er hhv. acceleration langs $x$-, $y$- og $z$-akserne samt tid i sekunder. Plot de tre accelerationskomponenter som funktion af tiden. | Indlæs datasættet. De fire variable er hhv. acceleration langs $x$-, $y$- og $z$-akserne samt tid i sekunder. Plot de tre accelerationskomponenter som funktion af tiden. | ||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | [[File:uge5fig5.png|frame|De tre accelerations-retninger.]] | ||
| + | Data indlæses med | ||
| + | :<code>data = importdata([datadir,'ipod_4.txt']);</code> | ||
| + | |||
| + | og man kan plotte de tre retnings-akser i samme figur med <code>subplot</code> | ||
| + | |||
| + | :<code>figure</code> | ||
| + | :<code>subplot(3,1,1)</code> | ||
| + | :<code>plot(data(:,4), data(:,1))</code> | ||
| + | :<code>title('acceleration x-akse (g)')</code> | ||
| + | :<code>subplot(3,1,2)</code> | ||
| + | :<code>plot(data(:,4), data(:,2))</code> | ||
| + | :<code>title('acceleration y-akse (g)')</code> | ||
| + | :<code>subplot(3,1,3)</code> | ||
| + | :<code>plot(data(:,4), data(:,3))</code> | ||
| + | :<code>title('acceleration z-akse (g)')</code> | ||
| + | |||
| + | Disse tre plots kan ses i figuren til højre. | ||
{{hidden end}} | {{hidden end}} | ||
| Line 196: | Line 214: | ||
Transponér input matricen sådan at den er $M \times N$, hvor $M$ svarer til antallet af parametre og $N$ antallet af målinger. Centrér derefter dataen ved først at beregne middelværdien for de fire parametre, og fratræk denne de enkelte komponenter. | Transponér input matricen sådan at den er $M \times N$, hvor $M$ svarer til antallet af parametre og $N$ antallet af målinger. Centrér derefter dataen ved først at beregne middelværdien for de fire parametre, og fratræk denne de enkelte komponenter. | ||
{{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | For at centrere dataen kan det være praktisk at bruge en kode a la | ||
| + | |||
:<code>data_center = data - repmat(middelværdierne, 1, antallet_af_målinger)</code> | :<code>data_center = data - repmat(middelværdierne, 1, antallet_af_målinger)</code> | ||
| + | |||
| + | Prøv at læse lidt om <code>repmat</code> i MATLAB hjælpen. | ||
{{hidden end}} | {{hidden end}} | ||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Transponeringen gøres med den simple <code>'</code> operator, og <code>size</code> kan bruges til at få <code>M</code> og <code>N</code>, | ||
| + | :<code>dat = data';</code> | ||
| + | :<code>[M N] = size(dat);</code> | ||
| + | |||
| + | Centreringen af dataen kan nu gøres som vist i hintet ovenfor, ved først at finde gennemsnittene i et nyt array, | ||
| + | |||
| + | :<code>m = mean(dat,2);</code> | ||
| + | |||
| + | og derefter bruge <code>repmat</code> til at lave et array der kan trækkes fra de oprindelige data (leg lidt med den, hvis du ikke forstår hvordan den virker). | ||
| + | |||
| + | :<code>dat = dat - repmat(m, 1, N);</code> | ||
{{hidden end}} | {{hidden end}} | ||
==== Del 2 ==== | ==== Del 2 ==== | ||
Beregn kovariansmatricen af den centrerede data, og beregn så egenværdierne og egenvektorerne af den, med den indbyggede funktion i MATLAB. Gem diagonalen af egenværdimatricen i en vektor ($M \times 1$). | Beregn kovariansmatricen af den centrerede data, og beregn så egenværdierne og egenvektorerne af den, med den indbyggede funktion i MATLAB. Gem diagonalen af egenværdimatricen i en vektor ($M \times 1$). | ||
| + | {{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Man kan finde egenværdier og egenvektorer for en matrice i MATLAB ved at bruge <code>eig</code> funktionen. Man kan trække diagonalen af en matrice ud til en vektor med <code>diag</code> funktionen. | ||
| + | {{hidden end}} | ||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Kovariansmatricen udregnes som sædvanligt, med | ||
| + | |||
| + | :<code>cor = cov(dat');</code> | ||
| + | |||
| + | Egenværdierne og egenvektorerne for denne matrice findes ved hjælp af den indbyggede funktion i MATLAB, der giver | ||
| + | |||
| + | :<code>[V E] = eig(cor);</code> | ||
| + | |||
| + | Her er <code>V</code> en matrice der indeholder egenvektorerne, mens <code>E</code> er en matrice der indeholder egenværdierne i diagonalen. Denne diagonal gemmes med | ||
| + | :<code>eval = diag(E);</code> | ||
{{hidden end}} | {{hidden end}} | ||
| Line 211: | Line 257: | ||
Sorter egenværdierne efter faldende orden, og gem de indekser som sorteringsmetoden retunerer i en vektor. | Sorter egenværdierne efter faldende orden, og gem de indekser som sorteringsmetoden retunerer i en vektor. | ||
{{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Læs lidt om <code>sort</code> funktionen i MATLAB hjælpen. Man kan få den til at spytte indekser ud ved hjælp kode på formen | ||
| + | |||
:<code>[smidvæk indices] = sort(egenværdier, 'descend')</code> | :<code>[smidvæk indices] = sort(egenværdier, 'descend')</code> | ||
{{hidden end}} | {{hidden end}} | ||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Dette gøres simpelthen med koden | ||
| + | :<code>[drop indices] = sort(eval, 'descend');</code> | ||
| + | |||
| + | hvor <code>drop</code> ikke skal bruges til noget videre. | ||
{{hidden end}} | {{hidden end}} | ||
| Line 220: | Line 272: | ||
Sorter egenvektorerne og egenværdierne med indeks-vektoren. | Sorter egenvektorerne og egenværdierne med indeks-vektoren. | ||
{{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Brug de indices som du gemte i del 3 til at bytte rundt på dine egenværdier og egenvektorer. Dette kan gøres med kode som | ||
| + | |||
:<code>egenvec = egenvec(:,indices); egenværdier = egenværdier(indices)</code> | :<code>egenvec = egenvec(:,indices); egenværdier = egenværdier(indices)</code> | ||
{{hidden end}} | {{hidden end}} | ||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Egenvektorerne i den ønskede rækkefølge findes med | ||
| + | |||
| + | :<code>egvec = V(:, indices);</code> | ||
| + | |||
| + | mens egenværdierne i samme rækkefølge findes med | ||
| + | :<code>eval = eval(indices);</code> | ||
{{hidden end}} | {{hidden end}} | ||
==== Del 5 ==== | ==== Del 5 ==== | ||
Projektér den oprindelige data langs den nye basis (egenvektor matricen). | Projektér den oprindelige data langs den nye basis (egenvektor matricen). | ||
| − | |||
| − | |||
| − | |||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | For at projicere skal man bare gange egenvektor matricen (transponeret, for at dimensionerne passer) sammen med dataen, som | ||
| + | :<code>data_pca = egvec' * dat;</code> | ||
{{hidden end}} | {{hidden end}} | ||
| Line 238: | Line 297: | ||
Plot hvert komponent af det transformerede datasæt som funktion af tiden. Ved at sammenligne værdierne fra egenvektorne med de fire plots, forklar hvad de enkelte komponenter beskriver. | Plot hvert komponent af det transformerede datasæt som funktion af tiden. Ved at sammenligne værdierne fra egenvektorne med de fire plots, forklar hvad de enkelte komponenter beskriver. | ||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | [[File:uge5fig6.png|frame|De fire komponenter efter PCA analysen.]] | ||
| + | Igen kan man plotte flere plots i samme figur ved at bruge <code>subplot</code>. | ||
| + | :<code>figure</code> | ||
| + | :<code>subplot(4,1,1)</code> | ||
| + | :<code>plot(data(:,4), data_pca(1, :))</code> | ||
| + | :<code>title('1. Komponent')</code> | ||
| + | :<code>subplot(4,1,2)</code> | ||
| + | :<code>plot(data(:,4), data_pca(2, :))</code> | ||
| + | :<code>title('2. Komponent')</code> | ||
| + | :<code>subplot(4,1,3)</code> | ||
| + | :<code>plot(data(:,4), data_pca(3, :))</code> | ||
| + | :<code>title('3. Komponent')</code> | ||
| + | :<code>subplot(4,1,4)</code> | ||
| + | :<code>plot(data(:,4), data_pca(4, :))</code> | ||
| + | :<code>title('4. Komponent')</code> | ||
{{hidden end}} | {{hidden end}} | ||
Revision as of 15:05, 7 March 2012
I denne uge skal I arbejde med lidt mere avanceret statisk, som en forsmag på hvad I kan lære i mere avancerede statistik-kurser, som f.eks. Anvendt Statistik, der afholdes i blok 1.
Som en forberedelse på at kunne lave disse opgaver, skal I læse et lille dokument skrevet af Morten Dam Jørgensen, der desuden også lavede nedenstående opgaver.
- Dokument om multivariat statistik: multivariatstatistik.pdf
Det kan også hjælpe at læse nogle Wikipedia-sider om emnerne, som f.eks.
- Multivariate analysis
- Covariance Matrix
- Correlations
- Autocorrelations (valgfri)
- Principal Component Analysis
- Linear models
- Non-linear models (kernel methods)
- Fast fourier transforms - cool blog om FFT (valgfri)
Contents |
Opgave 1 - Lineær korrelation
Disse øvelser viser hvordan lineære korrelationer kan beregnes og visualiseres, metoder som er anvendelige på det meste data med flere parametre.
Spørgsmål 1
Start med at indlæse datafilen, og plot så populationen i forhold til landenes størrelse.
Datafilen kan indlæses med koden
lande = importdata('lande.txt',';');
For nemmere at kunne arbejde med data sorteres de nu i rækkefølge efter landeareal, og population og areal skrives ind i hvert sit array:
sorted = sortrows(lande.data,1);A = sorted(:,1);P = sorted(:,2);
Plottet laves med
figureplot(A,P,'.')xlabel('lands størrelse [miles^2]')ylabel('antal indbyggere')title('Lineær sammenhæng')
Dette plot kan ses her til højre.
Spørgsmål 2
Beregn den linære korrelation manuelt (altså uden at bruge de indbyggede MATLAB funktioner til at gøre det). Er de to variable korrelerede?
Beregn først kovarians matricen (ligning 1 i multivariatstatistik.pdf dokumentet).
Covariansen mellem to vektorer er givet ved $\Sigma_{i,j} = \text{cov}(X_i,X_j) = E[(X_i-\mu_i)(X_j-\mu_j)]$, hvor $E[\cdot]$ er forventningsværdien - simpelthen gennemsnittet. Dermed kan man manuelt udregne covariansmatricen ved først at udregne
X1 = A - mean(A);X2 = P - mean(P);
og kan man simpelthen manuelt indsætte i kovarians matricen,
C_man = [ mean( X1 .* X1 ) mean( X1 .* X2 ) ; ...mean( X2 .* X1 ) mean( X2 .* X2 ) ];
Tilsvarende kan man manuelt finde den lineære korrelation med
r_man = mean( X1 .* X2 ) / ( std(A) * std(P) );
Værdien af r_man er ca. 0.45, så de variable er korrelerede, men ikke super-godt.
Spørgsmål 3
Beregn kovariansmatricen og korrelationsmatricen med MATLAB's indbyggede funktioner, og sammenlign resultatet med dine egne beregninger.
Læs om funktionerne cov og corr i MATLAB hjælpen.
Man bruger simpelthen de to funktioner cov og corr på A og P vektorerne,
C_aut = cov(A,P);r_aut = corr(A,P);
Spørgsmål 4
Tag logaritmen af begge værdier, og plot resultatet igen. Diskutér forskellen - er korrelationen tydeligere nu? Beregn korrelationen for de logaritmiske værdier. Hvorfor er korrelationen anderledes end i spørgsmål 2?
Man plotter simpelthen
figureplot(log(A),log(P),'.')xlabel('log( lands størrelse [miles^2] )')ylabel('log( antal indbyggere )')title('Dobbeltlogaritmisk sammenhæng')
Nu er det meget nemmere at se på data, da den tydeligvis er mere eksponentielt fordelt. Ud fra figuren forventer man også at korrelationen mellem de logaritmiske vektorer er mere lineær, da den faktisk ser lineær ud nu!
C_log = cov(log(A),log(P));r_log = corr(log(A),log(P));
Det viser sig at r_log er omkring 0.86, hvilket præcis er som forventet - korrelationen er bedre for de logaritmiske.
Spørgsmål 5
Lav et lineært fit af resultatet i spørgsmål 4. Hvor godt er fittet? Beskriver en lineær relation forholdet?
Fittet laves bare med
[cfun good] = fit(log(A),log(P),'poly1');
og kan plottes oven i den forrige figur med
hold onplot(log(A),cfun(log(A)),'-g')
For at finde ud af hvor godt fittet er, kan man udregne $\chi^2$ for det. Man kan også bruge den $R^2$ værdi som fit funktionen giver. Denne er givet i
good.rsquare;
Denne viser sig at være meget tæt på 1, hvilket fortæller at fittet er ret godt.
Altså er en lineær relation god til at beskrive forholdet mellem logaritmen af antallet af indbyggere i et lang og logaritmen af arealet af landet.
Opgave 2 - Flere korrelationer
Disse øvelser viser mere med korrelationer.
- Du skal starte med at hente datasættet opg2data.txt.
Spørgsmål 1
Indlæs datasættet og beregn korrelationerne mellem de to variable. Er variablene korrelerede?
Først indlæses datasættet med
tal = importdata([datadir,'opg2data.txt'],',');x = tal(:,1);y = tal(:,2);
Korrelationerne mellem de to variable findes med de indbyggede MATLAB funktioner,
C = cov(x,y);r = corr(x,y);
Det viser sig at der er cirka 1.1 % korrelation mellem variablene, og derfor er de slet ikke korrelerede!
Spørgsmål 2
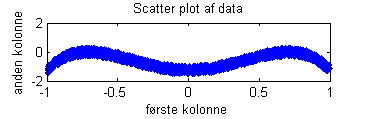
Lav et scatter plot af de to variable. Ved visuel inspektion, forklar hvorfor der ikke var en korrelation mellem de to akser i beregningen.
Plottet laves simpelthen med koden
figureplot(x,y,'.')xlabel('data fra første kolonne')ylabel('data fra anden kolonne')title('Scatter plot af data')
Dette plot er vist her til højre.
Det er tydeligt at se at der er en eller anden sammenhæng mellem de to akser, men den er absolut ikke lineær. Den lineære korrelation tager kun (logisk nok) linearitet med i beregningen, så alle højere ordens korrelationer bliver ikke fundet. For at kunne se højere ordens korrelationer skal man bruge mere avancerede statistiske værktøjer, som der bliver taget hul på i næste opgave.
Spørgsmål 3
Datasættet er genereret med følgende udtryk:
n = 2000;x = linspace(-1, 1, n);y = - 5 * (x.^2 - 1/2).^2 + unifrnd(-1, 1, [1 n])/3;
Der er tydeligvis en afhængighed mellem $x$- og $y$-aksen. I hvilke tilfælde vil en lineær korrelation være et acceptabelt mål for korrelationen mellem to værdier?
Lineær korrelation er et acceptabelt mål for korrelation i tilfælde hvor der er overordnet linearitet, uden symmetrier og højere-ordens effekter.
Opgave 3 - Principal component analysis
Disse øvelser handler om radial acceleration (med Principal Component Analysis - PCA).
- Du skal starte med at hente datasættet ipod_4.txt, der er et datasæt taget med app'en iSeismometer på en Ipod Touch som del af et eksperiment på kurset i 2011.
Spørgsmål 1
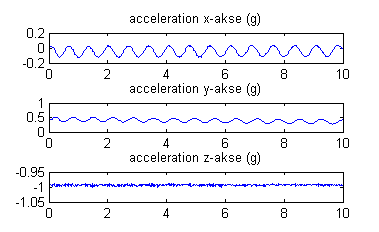
Indlæs datasættet. De fire variable er hhv. acceleration langs $x$-, $y$- og $z$-akserne samt tid i sekunder. Plot de tre accelerationskomponenter som funktion af tiden.
Data indlæses med
data = importdata([datadir,'ipod_4.txt']);
og man kan plotte de tre retnings-akser i samme figur med subplot
figuresubplot(3,1,1)plot(data(:,4), data(:,1))title('acceleration x-akse (g)')subplot(3,1,2)plot(data(:,4), data(:,2))title('acceleration y-akse (g)')subplot(3,1,3)plot(data(:,4), data(:,3))title('acceleration z-akse (g)')
Disse tre plots kan ses i figuren til højre.
Spørgsmål 2
I dette spørgsmål skal du finde de dominerende komponenter, ved at benytte PCA metoden beskrevet afsnit 2 i multivariatstatistik.pdf dokumentet. For at hjælpe dig lidt på vej er spørgsmålet delt op i mindre dele:
Del 1
Transponér input matricen sådan at den er $M \times N$, hvor $M$ svarer til antallet af parametre og $N$ antallet af målinger. Centrér derefter dataen ved først at beregne middelværdien for de fire parametre, og fratræk denne de enkelte komponenter.
For at centrere dataen kan det være praktisk at bruge en kode a la
data_center = data - repmat(middelværdierne, 1, antallet_af_målinger)
Prøv at læse lidt om repmat i MATLAB hjælpen.
Transponeringen gøres med den simple ' operator, og size kan bruges til at få M og N,
dat = data';[M N] = size(dat);
Centreringen af dataen kan nu gøres som vist i hintet ovenfor, ved først at finde gennemsnittene i et nyt array,
m = mean(dat,2);
og derefter bruge repmat til at lave et array der kan trækkes fra de oprindelige data (leg lidt med den, hvis du ikke forstår hvordan den virker).
dat = dat - repmat(m, 1, N);
Del 2
Beregn kovariansmatricen af den centrerede data, og beregn så egenværdierne og egenvektorerne af den, med den indbyggede funktion i MATLAB. Gem diagonalen af egenværdimatricen i en vektor ($M \times 1$).
Man kan finde egenværdier og egenvektorer for en matrice i MATLAB ved at bruge eig funktionen. Man kan trække diagonalen af en matrice ud til en vektor med diag funktionen.
Kovariansmatricen udregnes som sædvanligt, med
cor = cov(dat');
Egenværdierne og egenvektorerne for denne matrice findes ved hjælp af den indbyggede funktion i MATLAB, der giver
[V E] = eig(cor);
Her er V en matrice der indeholder egenvektorerne, mens E er en matrice der indeholder egenværdierne i diagonalen. Denne diagonal gemmes med
eval = diag(E);
Del 3
Sorter egenværdierne efter faldende orden, og gem de indekser som sorteringsmetoden retunerer i en vektor.
Læs lidt om sort funktionen i MATLAB hjælpen. Man kan få den til at spytte indekser ud ved hjælp kode på formen
[smidvæk indices] = sort(egenværdier, 'descend')
Dette gøres simpelthen med koden
[drop indices] = sort(eval, 'descend');
hvor drop ikke skal bruges til noget videre.
Del 4
Sorter egenvektorerne og egenværdierne med indeks-vektoren.
Brug de indices som du gemte i del 3 til at bytte rundt på dine egenværdier og egenvektorer. Dette kan gøres med kode som
egenvec = egenvec(:,indices); egenværdier = egenværdier(indices)
Egenvektorerne i den ønskede rækkefølge findes med
egvec = V(:, indices);
mens egenværdierne i samme rækkefølge findes med
eval = eval(indices);
Del 5
Projektér den oprindelige data langs den nye basis (egenvektor matricen).
For at projicere skal man bare gange egenvektor matricen (transponeret, for at dimensionerne passer) sammen med dataen, som
data_pca = egvec' * dat;
Spørgsmål 3
Plot hvert komponent af det transformerede datasæt som funktion af tiden. Ved at sammenligne værdierne fra egenvektorne med de fire plots, forklar hvad de enkelte komponenter beskriver.
Igen kan man plotte flere plots i samme figur ved at bruge subplot.
figuresubplot(4,1,1)plot(data(:,4), data_pca(1, :))title('1. Komponent')subplot(4,1,2)plot(data(:,4), data_pca(2, :))title('2. Komponent')subplot(4,1,3)plot(data(:,4), data_pca(3, :))title('3. Komponent')subplot(4,1,4)plot(data(:,4), data_pca(4, :))title('4. Komponent')
Spørgsmål 4
(Frivillig) Benyt MATLABs indbyggede PCA rutiner i stedet:
[C, latent, explained] = pcacov(cov(data'))biplot(egenvec(:,1:2), 'scores', signals(1:2,:)', 'varlabels',datalabels)
Spørgsmål 5
(Frivillig) PCA teknikken afhænger af lineære relationer mellem de forskellige variable. Der findes en anden metode til ikke-lineære data, der benytter det såkaldte "kernel-kneb". I zip-filen medfølger en funktion kaldet "kernelpca_tutorial.m", gentag spørgsmål 4 for resultatet fra funktionen.
Mere info: http://en.wikipedia.org/wiki/Kernel_principal_component_analysis
Samlede løsninger
- Et samlet dokument med MATLAB kode til at løse alle opgaverne ovenfor kan hentes her: opgaver_uge5_kovarians.m