opgaver:Uge3
Pia Jensen (Talk | contribs) |
m |
||
| (13 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | I denne opgave skal I arbejde med fitning som forklaret i Taylor kapitel 8. I skal her selv lave et datasæt, og lærer derfor også hvordan man genererer tilfældige tal i MATLAB. Opgave 2 og 3 er uafhængige, og kan laves i den rækkefølge I har lyst til. | + | I denne opgave skal I arbejde med fitning som forklaret i Barlow kapitel 6<!--Taylor kapitel 8-->. I skal her selv lave et datasæt, og lærer derfor også hvordan man genererer tilfældige tal i MATLAB. Opgave 2 og 3 er uafhængige, og kan laves i den rækkefølge I har lyst til. |
| Line 5: | Line 5: | ||
=== Spørgsmål 1 - Lineær model === | === Spørgsmål 1 - Lineær model === | ||
| − | Antag at I har en lineær model som i Taylor afsnit 8.2, | + | |
| + | Antag at I har en lineær model som i Barlow afsnit 6.2<!--Taylor afsnit 8.2-->, | ||
:$y = A + B x .$ | :$y = A + B x .$ | ||
| Line 11: | Line 12: | ||
Vælg passende værdier af <code>A</code> og <code>B</code> og lav en vektor <code>x</code> med målepunkter, f.eks. <code>A = 0</code>, <code>B = 1</code>, <code>x = -2:0.1:2</code>. Lav nu en vektor med den "sande" <code>y</code> ud fra modellen. Vælg en usikkerhed for målingerne, og læg en normalfordelt støj til hver måling - brug MATLAB funktionen <code>randn()</code>. Plot målingerne (med usikkerhederne) og den "sande" model i samme plot. | Vælg passende værdier af <code>A</code> og <code>B</code> og lav en vektor <code>x</code> med målepunkter, f.eks. <code>A = 0</code>, <code>B = 1</code>, <code>x = -2:0.1:2</code>. Lav nu en vektor med den "sande" <code>y</code> ud fra modellen. Vælg en usikkerhed for målingerne, og læg en normalfordelt støj til hver måling - brug MATLAB funktionen <code>randn()</code>. Plot målingerne (med usikkerhederne) og den "sande" model i samme plot. | ||
| − | Beregn lineær regression ud fra | + | Beregn lineær regression ud fra Barlow og find de estimerede værdier for <code>A</code> og <code>B</code>, og beregn den fittede modelværdi, <code>y_fit</code>. Plot <code>y_fit</code> oveni det forrige plot og se hvor godt fittet er. Beregn den reducerede $\chi^2$, givet ved |
:$\dfrac{\chi^2}{N-P} ,$ | :$\dfrac{\chi^2}{N-P} ,$ | ||
| Line 17: | Line 18: | ||
hvor $N$ er antal datapunkter og $P$ er antal fit-parametre. | hvor $N$ er antal datapunkter og $P$ er antal fit-parametre. | ||
{{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| − | Start med at udregne selve den teoretiske linie <code>y_model</code>, ved at definere <code>A</code>, <code>B</code> og din <code>x</code>-akse. Definér derefter en <code>sigma</code> du vil bruge som din usikkerhed. Så kan din y udregnes som <code>y_model</code> plus en vektor der består af Gaussisk fordelte tal med spredning <code>sigma</code> og centrum nul. | + | Start med at udregne selve den teoretiske linie <code>y_model</code>, ved at definere <code>A</code>, <code>B</code> og din <code>x</code>-akse. Definér derefter en <code>sigma</code> du vil bruge som din usikkerhed. Så kan din $y$ udregnes som <code>y_model</code> plus en vektor der består af Gaussisk fordelte tal med spredning <code>sigma</code> og centrum nul. |
{{hidden end}} | {{hidden end}} | ||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| Line 31: | Line 32: | ||
:<code>y_model = A_model + B_model*x;</code> | :<code>y_model = A_model + B_model*x;</code> | ||
| − | + | Du kan nu lave en model med støj på punkterne med spredning givet ved <code>sigma</code> du definerede tidligere, ved at bruge <code>randn()</code> funktionen | |
| − | :<code> | + | :<code>y = y_model + sigma*randn(size(y_model));</code> |
| − | + | Nu kan du plotte din model sammen med dine "målepunkter" (bemærk at for at få errorbars på er man nødt til at lave en vektor med samme længde som $x$ og $y$, som indeholder $\sigma$ for hver $y$-værdi - men da $\sigma$ er den samme for alle punkterne kan man bare bruge <code>ones()</code> funktionen), | |
| − | : | + | [[File:uge3fig1.png|frame|Modellen vist som en linie, sammen med genererede data med støj.]] |
| − | + | ||
| − | + | ||
:<code>figure</code> | :<code>figure</code> | ||
| − | :<code>errorbar(x,y, | + | :<code>errorbar(x,y,sigma*ones(size(y_model)),'bo','MarkerFaceColor', [0.4 0.4 0.8],...</code> |
::<code> 'MarkerEdgeColor',[0.4 0.4 0.8])</code> | ::<code> 'MarkerEdgeColor',[0.4 0.4 0.8])</code> | ||
:<code>hold on</code> | :<code>hold on</code> | ||
| Line 50: | Line 49: | ||
En sådan figur er vist her til højre. | En sådan figur er vist her til højre. | ||
| − | :<code></code> | + | |
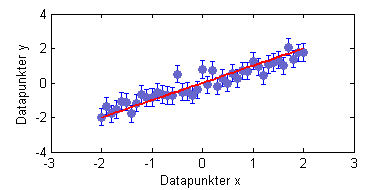
| + | [[File:uge3fig2.png|frame|Modellen og datapunkterne med støj, nu med en fit-linie (grøn).]] | ||
| + | Regressionsparametrene kan udregnes med | ||
| + | |||
| + | :<code>N = length(x);</code> | ||
| + | :<code>Sy = sum(y);</code> | ||
| + | :<code>Sx = sum(x);</code> | ||
| + | :<code>Sxx = sum(x.^2);</code> | ||
| + | :<code>Sxy = sum(x.*y);</code> | ||
| + | :<code>Delta = N*Sxx-Sx^2;</code> | ||
| + | :<code>A_fit = ( Sxx*Sy - Sx*Sxy )/Delta;</code> | ||
| + | :<code>B_fit = ( N*Sxy - Sx*Sy )/Delta;</code> | ||
| + | |||
| + | og fit-linien er så fundet til at være | ||
| + | |||
| + | :<code>y_fit = A_fit + B_fit*x;</code> | ||
| + | |||
| + | Denne linie plottes oven på model-linien og punkterne med | ||
| + | |||
| + | :<code>plot(x,y_fit,'g-','LineWidth',2)</code> | ||
| + | |||
| + | og så får man figuren til højre. Den reducerede $\chi^2$ findes til sidst med koden | ||
| + | |||
| + | :<code>chi2 = sum((y-y_fit).^2 ./ (sigma*ones(size(y)).^2);</code> | ||
| + | :<code>chi2red = chi2/(N-2);</code> | ||
{{hidden end}} | {{hidden end}} | ||
| + | |||
| + | ==== 1b - Andenordenskorrektion ==== | ||
| + | |||
| + | Lav ny en ny serie af datapunkter ud fra forskriften | ||
| + | |||
| + | :$ y = A + B x + C x^2$ | ||
| + | |||
| + | Vælg <code>C = 0.3</code>, for samme interval af x-værdier. Udregn nu det reducerede $\chi^2$ mellem det gamle fit og de nye data. Bliver det værre eller bedre? | ||
| + | |||
| + | Lav nu et plot af residuals, Residuals er afvigelsen mellem data- og fitværdier for hvert målepunkt. Disse kan bruges til at opdage systematisk afvigelser, hvilket kan indikere at fitmodellen er utilstrækkelig. | ||
| + | |||
| + | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Først laves en ny serie y-modelværdier: | ||
| + | :<code>C_model = 0.3;</code> | ||
| + | :<code>y_model_ny = A_model + B_model*x + C_model*x.^2;</code> | ||
| + | Dernæst laves nye værdier med støj: | ||
| + | :<code>y_ny = y_model_ny + sigma_y.*randn(size(y_model));</code> | ||
| + | |||
| + | Vi kan derefter plotte de nye værdier sammen med de gamle samt både den gamle og nye model samt fittet til de lineære data. Du kan evt. supplere med et lineært fit til de nye data. | ||
| + | :<code>figure</code> | ||
| + | :<code>errorbar(x,y,sigma_y,'bo','MarkerFaceColor', [0.4 0.4 0.8],...</code> | ||
| + | :<code>'MarkerEdgeColor',[0.4 0.4 0.8])</code> | ||
| + | :<code>hold on</code> | ||
| + | :<code>errorbar(x,y_ny,sigma_y,'bo','MarkerFaceColor', [0.4 0.4 0.4],...</code> | ||
| + | :<code>'MarkerEdgeColor',[0.4 0.4 0.4])</code> | ||
| + | :<code>plot(x,y_model,'r-','LineWidth',2)</code> | ||
| + | :<code>plot(x,y_model_ny,'k-','LineWidth',2)</code> | ||
| + | :<code>y_fit = A_fit + B_fit*x;</code> | ||
| + | :<code>plot(x,y_fit,'g-','LineWidth',2)</code> | ||
| + | :<code>xlabel('Datapunkter x')</code> | ||
| + | :<code>ylabel('Datapunkter y')</code> | ||
| + | :<code>hold off</code> | ||
| + | Herefter udregnes det nye reducerede $\chi^2$-værdi. | ||
| + | :<code>chi2_ny = sum((y_ny-y_fit).^2 ./ sigma_y.^2);</code> | ||
| + | :<code>chi2red_ny = chi2_ny/(N-2);</code> | ||
| + | |||
| + | Til sidst plottes residuals. | ||
| + | :<code>figure</code> | ||
| + | :<code>bar(x,y_ny-y_fit)</code> | ||
| + | :<code>hold on</code> | ||
| + | :<code>bar(x,y-y_fit,'r','BarWidth',0.5)</code> | ||
| + | {{hidden end}} | ||
| + | |||
=== Spørgsmål 2 - Gentagelse === | === Spørgsmål 2 - Gentagelse === | ||
Gentag dette "numeriske forsøg" et antal gange (f.eks. 100) og gem for hver gang fittets parametre. Brug <code>hist()</code> til at finde fordelingen af <code>A</code>, <code>B</code>, og reduceret $\chi^2$. Sammenlign med den estimerede usikkerhed på <code>A</code> og <code>B</code>, og undersøg evt. korrelationen mellem <code>A</code> og <code>B</code> (plot f.eks. <code>A</code> vs. <code>B</code>). | Gentag dette "numeriske forsøg" et antal gange (f.eks. 100) og gem for hver gang fittets parametre. Brug <code>hist()</code> til at finde fordelingen af <code>A</code>, <code>B</code>, og reduceret $\chi^2$. Sammenlign med den estimerede usikkerhed på <code>A</code> og <code>B</code>, og undersøg evt. korrelationen mellem <code>A</code> og <code>B</code> (plot f.eks. <code>A</code> vs. <code>B</code>). | ||
{{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Hint|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Start med at bruge den kode du lavede til spørgsmål a, og lav så et loop uden om det hele. I slutningen af loopet skal du gemme <code>A</code>, <code>B</code> og din reducerede $\chi^2$ i et array - så du kan plotte alle værdierne bagefter. | ||
| + | {{hidden end}} | ||
| + | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | Man kan genbruge al sin kode fra spørgsmål a til at lave sit loop. Definitionen af <code>A_model</code>, <code>B_model</code>, <code>sigma</code>, <code>x</code> og <code>y_model</code> får lov til at blive, og så skal man forberede sit loop med antal gange man vil køre det, og tre lister til at gemme de resultater man får, | ||
| + | |||
| + | :<code>N_iter = 100;</code> | ||
| + | :<code>A_liste = zeros(1,N_iter);</code> | ||
| + | :<code>B_liste = zeros(1,N_iter);</code> | ||
| + | :<code>chi2_liste = zeros(1,N_iter);</code> | ||
| + | |||
| + | Herefter starter man sit loop lige før udregningen af <code>y</code>, således at hvert loop laver en ny række punkter med anderledes støj. | ||
| + | |||
| + | :<code>for i = 1:N_iter</code> | ||
| + | ::<code>y = y_model + sigma*randn(size(y_model));</code> | ||
| + | ::<code>...</code> | ||
| + | |||
| + | Udregningen af regressionsparametrene er helt som før. Til sidst skal man gemme sine resultater i sine arrays, | ||
| − | + | ::<code>...</code> | |
| + | ::<code>A_liste(i) = A_fit;</code> | ||
| + | ::<code>B_liste(i) = B_fit;</code> | ||
| + | ::<code>chi2_liste(i) = chi2red;</code> | ||
| + | :<code>end</code> | ||
| + | Disse arrays kan man nu se lidt på. F.eks. kan man lave histogrammer eller korrelationsplots med <code>hist</code> eller <code>scatter</code>. | ||
{{hidden end}} | {{hidden end}} | ||
| Line 64: | Line 152: | ||
Prøv at anvende MATLABs fittefunktion <code>fit(x,y,'funktion')</code> og sammenlign med jeres egen lineære regression. | Prøv at anvende MATLABs fittefunktion <code>fit(x,y,'funktion')</code> og sammenlign med jeres egen lineære regression. | ||
{{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | {{hidden begin|toggle=right|title=Løsning|titlestyle=background:#ccccff|bg2=#eeeeee}} | ||
| + | [[File:uge3fig3.png|frame|Modellen og datapunkterne med støj, plottet med fit-linien (grøn).]] | ||
| + | Den automatiske fitning i MATLAB kan bruges med koden | ||
| + | :<code>[res good] = fit(x',y','poly1')</code> | ||
| + | |||
| + | her er <code>poly1</code> den indbyggede lineære funktion, men man kan også selv skrive sin funktion ind (se på MATLAB hjælp siden for <code>fit</code>). Fittet kan nu plottes sammen med datapunkterne og model-linien med | ||
| + | |||
| + | :<code>figure</code> | ||
| + | :<code>errorbar(x,y,sigma*ones(size(y),'ro')</code> | ||
| + | :<code>hold on</code> | ||
| + | :<code>plot(x,y_model,'b-')</code> | ||
| + | :<code>plot(x,res(x),'g-')</code> | ||
| + | :<code>xlabel('Datapunkter x')</code> | ||
| + | :<code>ylabel('Datapunkter y')</code> | ||
| + | |||
| + | Denne figur kan ses til højre. | ||
{{hidden end}} | {{hidden end}} | ||
| + | |||
| + | |||
| + | |||
| + | == Samlede løsninger == | ||
| + | * Et samlet dokument med MATLAB kode til at løse alle opgaverne ovenfor kan hentes her: [[Media:opgaver_uge3_fits_ny.m|opgaver_uge3_fits_ny.m]] | ||
Latest revision as of 15:38, 1 May 2015
I denne opgave skal I arbejde med fitning som forklaret i Barlow kapitel 6. I skal her selv lave et datasæt, og lærer derfor også hvordan man genererer tilfældige tal i MATLAB. Opgave 2 og 3 er uafhængige, og kan laves i den rækkefølge I har lyst til.
Contents |
Opgave 1 - Fitning
Spørgsmål 1 - Lineær model
Antag at I har en lineær model som i Barlow afsnit 6.2,
- $y = A + B x .$
Vælg passende værdier af A og B og lav en vektor x med målepunkter, f.eks. A = 0, B = 1, x = -2:0.1:2. Lav nu en vektor med den "sande" y ud fra modellen. Vælg en usikkerhed for målingerne, og læg en normalfordelt støj til hver måling - brug MATLAB funktionen randn(). Plot målingerne (med usikkerhederne) og den "sande" model i samme plot.
Beregn lineær regression ud fra Barlow og find de estimerede værdier for A og B, og beregn den fittede modelværdi, y_fit. Plot y_fit oveni det forrige plot og se hvor godt fittet er. Beregn den reducerede $\chi^2$, givet ved
- $\dfrac{\chi^2}{N-P} ,$
hvor $N$ er antal datapunkter og $P$ er antal fit-parametre.
Start med at udregne selve den teoretiske linie y_model, ved at definere A, B og din x-akse. Definér derefter en sigma du vil bruge som din usikkerhed. Så kan din $y$ udregnes som y_model plus en vektor der består af Gaussisk fordelte tal med spredning sigma og centrum nul.
Start med at definere de to konstanter, din x-akse og den usikkerhed du gerne vil have på punkterne, her f.eks.
A_model = 0;B_model = 1;sigma = 0.5;x = -2:0.1:2;
Nu kan du udregne modellens y-værdi direkte ved
y_model = A_model + B_model*x;
Du kan nu lave en model med støj på punkterne med spredning givet ved sigma du definerede tidligere, ved at bruge randn() funktionen
y = y_model + sigma*randn(size(y_model));
Nu kan du plotte din model sammen med dine "målepunkter" (bemærk at for at få errorbars på er man nødt til at lave en vektor med samme længde som $x$ og $y$, som indeholder $\sigma$ for hver $y$-værdi - men da $\sigma$ er den samme for alle punkterne kan man bare bruge ones() funktionen),
figureerrorbar(x,y,sigma*ones(size(y_model)),'bo','MarkerFaceColor', [0.4 0.4 0.8],...'MarkerEdgeColor',[0.4 0.4 0.8])
hold onplot(x,y_model,'r-','LineWidth',2)xlabel('Datapunkter x')ylabel('Datapunkter y')
En sådan figur er vist her til højre.
Regressionsparametrene kan udregnes med
N = length(x);Sy = sum(y);Sx = sum(x);Sxx = sum(x.^2);Sxy = sum(x.*y);Delta = N*Sxx-Sx^2;A_fit = ( Sxx*Sy - Sx*Sxy )/Delta;B_fit = ( N*Sxy - Sx*Sy )/Delta;
og fit-linien er så fundet til at være
y_fit = A_fit + B_fit*x;
Denne linie plottes oven på model-linien og punkterne med
plot(x,y_fit,'g-','LineWidth',2)
og så får man figuren til højre. Den reducerede $\chi^2$ findes til sidst med koden
chi2 = sum((y-y_fit).^2 ./ (sigma*ones(size(y)).^2);chi2red = chi2/(N-2);
1b - Andenordenskorrektion
Lav ny en ny serie af datapunkter ud fra forskriften
- $ y = A + B x + C x^2$
Vælg C = 0.3, for samme interval af x-værdier. Udregn nu det reducerede $\chi^2$ mellem det gamle fit og de nye data. Bliver det værre eller bedre?
Lav nu et plot af residuals, Residuals er afvigelsen mellem data- og fitværdier for hvert målepunkt. Disse kan bruges til at opdage systematisk afvigelser, hvilket kan indikere at fitmodellen er utilstrækkelig.
Først laves en ny serie y-modelværdier:
C_model = 0.3;y_model_ny = A_model + B_model*x + C_model*x.^2;
Dernæst laves nye værdier med støj:
y_ny = y_model_ny + sigma_y.*randn(size(y_model));
Vi kan derefter plotte de nye værdier sammen med de gamle samt både den gamle og nye model samt fittet til de lineære data. Du kan evt. supplere med et lineært fit til de nye data.
figureerrorbar(x,y,sigma_y,'bo','MarkerFaceColor', [0.4 0.4 0.8],...'MarkerEdgeColor',[0.4 0.4 0.8])hold onerrorbar(x,y_ny,sigma_y,'bo','MarkerFaceColor', [0.4 0.4 0.4],...'MarkerEdgeColor',[0.4 0.4 0.4])plot(x,y_model,'r-','LineWidth',2)plot(x,y_model_ny,'k-','LineWidth',2)y_fit = A_fit + B_fit*x;plot(x,y_fit,'g-','LineWidth',2)xlabel('Datapunkter x')ylabel('Datapunkter y')hold off
Herefter udregnes det nye reducerede $\chi^2$-værdi.
chi2_ny = sum((y_ny-y_fit).^2 ./ sigma_y.^2);chi2red_ny = chi2_ny/(N-2);
Til sidst plottes residuals.
figurebar(x,y_ny-y_fit)hold onbar(x,y-y_fit,'r','BarWidth',0.5)
Spørgsmål 2 - Gentagelse
Gentag dette "numeriske forsøg" et antal gange (f.eks. 100) og gem for hver gang fittets parametre. Brug hist() til at finde fordelingen af A, B, og reduceret $\chi^2$. Sammenlign med den estimerede usikkerhed på A og B, og undersøg evt. korrelationen mellem A og B (plot f.eks. A vs. B).
Start med at bruge den kode du lavede til spørgsmål a, og lav så et loop uden om det hele. I slutningen af loopet skal du gemme A, B og din reducerede $\chi^2$ i et array - så du kan plotte alle værdierne bagefter.
Man kan genbruge al sin kode fra spørgsmål a til at lave sit loop. Definitionen af A_model, B_model, sigma, x og y_model får lov til at blive, og så skal man forberede sit loop med antal gange man vil køre det, og tre lister til at gemme de resultater man får,
N_iter = 100;A_liste = zeros(1,N_iter);B_liste = zeros(1,N_iter);chi2_liste = zeros(1,N_iter);
Herefter starter man sit loop lige før udregningen af y, således at hvert loop laver en ny række punkter med anderledes støj.
for i = 1:N_itery = y_model + sigma*randn(size(y_model));...
Udregningen af regressionsparametrene er helt som før. Til sidst skal man gemme sine resultater i sine arrays,
...A_liste(i) = A_fit;B_liste(i) = B_fit;chi2_liste(i) = chi2red;
end
Disse arrays kan man nu se lidt på. F.eks. kan man lave histogrammer eller korrelationsplots med hist eller scatter.
Spørgsmål 3 - Automatisk fitning i MATLAB
Prøv at anvende MATLABs fittefunktion fit(x,y,'funktion') og sammenlign med jeres egen lineære regression.
Den automatiske fitning i MATLAB kan bruges med koden
[res good] = fit(x',y','poly1')
her er poly1 den indbyggede lineære funktion, men man kan også selv skrive sin funktion ind (se på MATLAB hjælp siden for fit). Fittet kan nu plottes sammen med datapunkterne og model-linien med
figureerrorbar(x,y,sigma*ones(size(y),'ro')hold onplot(x,y_model,'b-')plot(x,res(x),'g-')xlabel('Datapunkter x')ylabel('Datapunkter y')
Denne figur kan ses til højre.
Samlede løsninger
- Et samlet dokument med MATLAB kode til at løse alle opgaverne ovenfor kan hentes her: opgaver_uge3_fits_ny.m